Περιεχόμενο

• Βήματα
• Συμβουλές

Η λογική συνάρτηση έχει τη μορφή y = N (x) / D (x), όπου N και D είναι πολυώνυμα. Για να σχεδιάσετε με ακρίβεια μια τέτοια συνάρτηση, χρειάζεστε καλή γνώση της άλγεβρας, συμπεριλαμβανομένων διαφορικών υπολογισμών. Εξετάστε το ακόλουθο παράδειγμα: y = (2Χ - 6Χ + 5)/(4Χ + 2).

Βήματα

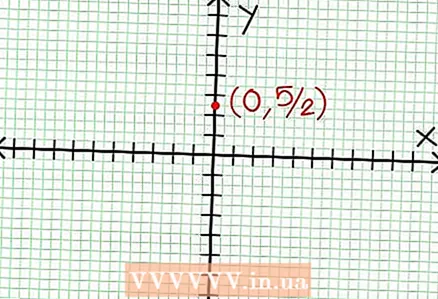1. 1 Βρείτε την παρεμβολή y του γραφήματος. Για να το κάνετε αυτό, αντικαταστήστε x = 0 στη συνάρτηση και λάβετε y = 5/2. Έτσι, το σημείο τομής του γραφήματος με τον άξονα Υ έχει συντεταγμένες (0, 5/2).Τοποθετήστε αυτό το σημείο στο επίπεδο συντεταγμένων.
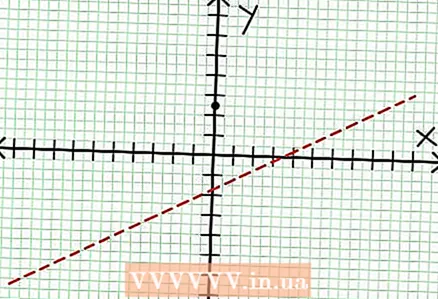2. 2 Βρείτε τα οριζόντια ασύμπτωτα. Διαιρέστε τον αριθμητή με τον παρονομαστή (σε μια στήλη) για να προσδιορίσετε τη συμπεριφορά του "y" με τιμές "x" που τείνουν στο άπειρο. Στο παράδειγμά μας, η διαίρεση θα είναι y = (1/2)Χ - (7/4) + 17/(8Χ + 4). Για μεγάλες θετικές ή αρνητικές τιμές "x" 17 / (8Χ + 4) τείνει στο μηδέν και το γράφημα προσεγγίζει την ευθεία που δίνει η συνάρτηση y = (1/2)Χ - (7/4). Χρησιμοποιώντας τη διακεκομμένη γραμμή, σχεδιάστε αυτήν τη συνάρτηση.
   • Εάν ο βαθμός του αριθμητή είναι μικρότερος από τον βαθμό του παρονομαστή, τότε δεν μπορείτε να διαιρέσετε τον αριθμητή με τον παρονομαστή και το ασύμπτωτο θα περιγραφεί από τη συνάρτηση στο = 0.
   • Εάν ο βαθμός του αριθμητή είναι ίσος με τον βαθμό του παρονομαστή, τότε το ασύμπτωτο είναι μια οριζόντια γραμμή ίση με την αναλογία των συντελεστών στο "x" στον υψηλότερο βαθμό.
   • Εάν ο βαθμός του αριθμητή είναι 1 μεγαλύτερος από τον βαθμό του παρονομαστή, τότε το ασύμπτωτο είναι μια κεκλιμένη ευθεία, η κλίση της οποίας είναι ίση με την αναλογία των συντελεστών στο "x" στον υψηλότερο βαθμό.
   • Εάν ο βαθμός του αριθμητή είναι μεγαλύτερος από τον βαθμό του παρονομαστή κατά 2, 3 κ.λπ., τότε για μεγάλες τιμές |NS| έννοια στο τείνουν στο άπειρο (θετικό ή αρνητικό) με τη μορφή τετραγώνου, κυβικού ή άλλου βαθμού πολυωνύμου. Σε αυτή την περίπτωση, πιθανότατα, δεν χρειάζεται να δημιουργήσετε ένα ακριβές γράφημα της συνάρτησης που λαμβάνεται διαιρώντας τον αριθμητή με τον παρονομαστή.
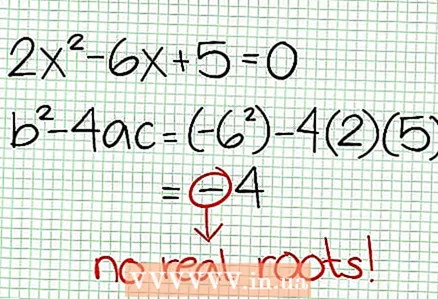3. 3 Βρείτε τα μηδενικά της συνάρτησης. Μια λογική συνάρτηση έχει μηδενικά όταν ο αριθμητής της είναι μηδέν, δηλαδή N (NS) = 0. Στο παράδειγμά μας, 2Χ - 6Χ + 5 = 0. Το διακριτικό αυτής της τετραγωνικής εξίσωσης: σι - 4μετα Χριστον = 6 - 4 * 2 * 5 = 36 - 40 = -4. Δεδομένου ότι το διακριτικό είναι αρνητικό, τότε N (NS), και ως εκ τούτου F (NS) δεν έχει πραγματικές ρίζες. Η γραφική παράσταση μιας λογικής συνάρτησης δεν τέμνει τον άξονα Χ. Αν η συνάρτηση έχει μηδενικά (ρίζες), τότε τα βάζουμε στο επίπεδο συντεταγμένων.
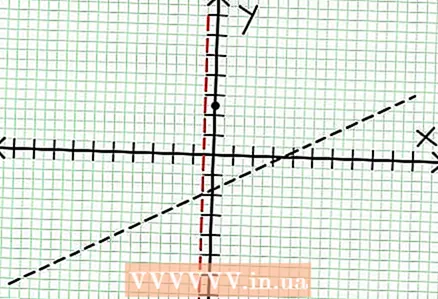4. 4 Βρείτε τις κάθετες ασύμπτωτες. Για να το κάνετε αυτό, ορίστε τον παρονομαστή στο μηδέν. Στο παράδειγμά μας, 4Χ + 2 = 0 και NS = -1/2. Σχεδιάστε το κάθετο ασύμπτωτο χρησιμοποιώντας τη διακεκομμένη γραμμή. Αν για κάποια αξία NS Ν (NS) = 0 και Δ (NS) = 0, τότε το κάθετο ασύμπτωτο είτε υπάρχει είτε δεν υπάρχει (πρόκειται για σπάνια περίπτωση, αλλά καλύτερα να το θυμάστε).
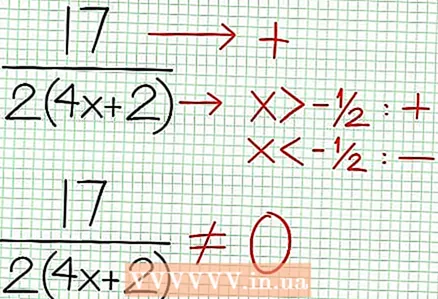5. 5 Κοιτάξτε το υπόλοιπο του αριθμητή διαιρούμενο με τον παρονομαστή. Είναι θετικό, αρνητικό ή μηδενικό; Στο παράδειγμά μας, το υπόλοιπο είναι 17, το οποίο είναι θετικό. Παρονομαστής 4Χ + 2 θετικά στα δεξιά του κάθετου ασύμπτωτου και αρνητικά στα αριστερά του. Αυτό σημαίνει ότι η γραφική παράσταση της λογικής συνάρτησης για μεγάλες θετικές τιμές NS προσεγγίζει το ασύμπτωτο από πάνω, και για μεγάλες αρνητικές τιμές NS - από κάτω. Από τις 17 / (8Χ + 4) δεν είναι ποτέ ίσο με το μηδέν, τότε το γράφημα αυτής της συνάρτησης δεν θα τέμνει ποτέ την ευθεία που καθορίζεται από τη συνάρτηση στο = (1/2)NS - (7/4).
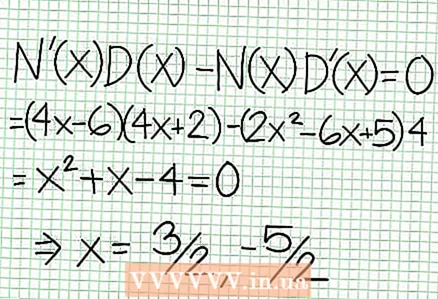6. 6 Βρείτε τοπικά άκρα. Υπάρχει ένα τοπικό άκρο για το Ν '(Χ) D (Χ) - Ν (Χ) D ’(Χ) = 0. Στο παράδειγμά μας, N ’(Χ) = 4Χ - 6 και Δ '(Χ) = 4. Ν ’(Χ) D (Χ) - Ν (Χ) D ’(Χ) = (4Χ - 6)(4Χ + 2) - (2Χ - 6Χ + 5)*4 = Χ + Χ - 4 = 0. Λύνοντας αυτήν την εξίσωση, βρίσκεις ότι Χ = 3/2 και Χ = -5/2. (Αυτές δεν είναι εντελώς ακριβείς τιμές, αλλά είναι κατάλληλες για την περίπτωσή μας όταν δεν απαιτείται υπερβολική ακρίβεια.)
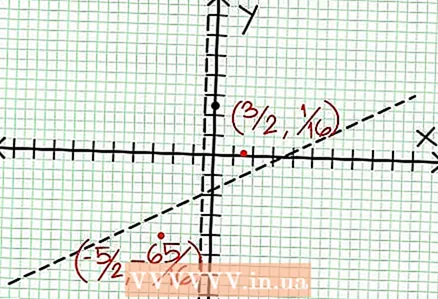7. 7 Βρείτε την τιμή στο για κάθε τοπικό άκρο. Για να το κάνετε αυτό, αντικαταστήστε τις τιμές NS στην αρχική λογική λειτουργία. Στο παράδειγμά μας, f (3/2) = 1/16 και f (-5/2) = -65/16. Αφήστε στην άκρη τα σημεία (3/2, 1/16) και (-5/2, -65/16) στο επίπεδο συντεταγμένων. Δεδομένου ότι οι υπολογισμοί βασίζονται σε κατά προσέγγιση τιμές (από το προηγούμενο βήμα), το ελάχιστο και το μέγιστο που βρέθηκαν δεν είναι επίσης απόλυτα ακριβή (αλλά πιθανώς πολύ κοντά στις ακριβείς τιμές). (Το σημείο (3/2, 1/16) είναι πολύ κοντά στο τοπικό ελάχιστο. Ξεκινώντας από το βήμα 3, γνωρίζουμε ότι στο πάντα θετικό για NS> -1/2 και βρήκαμε μια μικρή τιμή (1/16). έτσι, η τιμή σφάλματος είναι εξαιρετικά μικρή σε αυτήν την περίπτωση.)
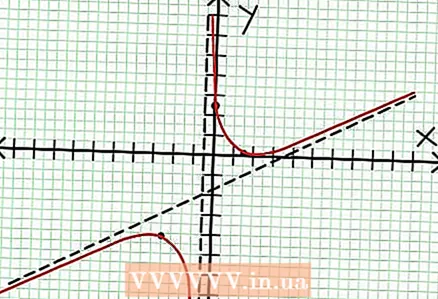8. 8 Συνδέστε τα εκκρεμή σημεία και επεκτείνετε ομαλά το γράφημα στα ασύμπτωτα (μην ξεχνάτε τη σωστή κατεύθυνση του γραφήματος που πλησιάζει τους ασύμπτωτους). Θυμηθείτε ότι το γράφημα δεν πρέπει να διασχίζει τον άξονα Χ (δείτε βήμα 3). Το γράφημα επίσης δεν τέμνεται με τις οριζόντιες και κάθετες ασύμπτωτες (βλέπε βήμα 5). Μην αλλάζετε την κατεύθυνση του γραφήματος παρά μόνο στα ακραία σημεία που βρέθηκαν στο προηγούμενο βήμα.

Συμβουλές

• Εάν ακολουθήσατε τα παραπάνω βήματα αυστηρά με τη σειρά, τότε δεν χρειάζεται να υπολογίσετε τα δεύτερα παράγωγα (ή παρόμοιες πολύπλοκες ποσότητες) για να δοκιμάσετε τη λύση σας.
• Εάν δεν χρειάζεται να υπολογίσετε τις τιμές των ποσοτήτων, μπορείτε να αντικαταστήσετε την εύρεση τοπικών ακραίων υπολογισμών υπολογίζοντας κάποια επιπλέον ζεύγη συντεταγμένων (NS, στο) μεταξύ κάθε ζεύγους ασύμπτωτων. Επιπλέον, εάν δεν σας ενδιαφέρει πώς λειτουργεί η περιγραφόμενη μέθοδος, τότε μην εκπλαγείτε γιατί δεν μπορείτε να βρείτε την παράγωγο και να λύσετε την εξίσωση Ν '(Χ) D (Χ) - Ν (Χ) D ’(Χ) = 0.
• Σε ορισμένες περιπτώσεις, θα πρέπει να εργαστείτε με πολυώνυμα υψηλότερης τάξης. Εάν δεν μπορείτε να βρείτε την ακριβή λύση χρησιμοποιώντας παραγοντοποίηση, τύπους κλπ., Τότε εκτιμήστε πιθανές λύσεις χρησιμοποιώντας αριθμητικές μεθόδους όπως η μέθοδος του Νεύτωνα.
• Σε σπάνιες περιπτώσεις, ο αριθμητής και ο παρονομαστής μοιράζονται έναν κοινό μεταβλητό παράγοντα. Σύμφωνα με τα βήματα που περιγράφονται, αυτό θα οδηγήσει στο μηδέν και ένα κάθετο ασύμπτωτο στο ίδιο σημείο. Ωστόσο, αυτό δεν είναι δυνατό και η εξήγηση είναι μία από τις ακόλουθες:
  • Μηδέν σε Β (NS) έχει μεγαλύτερη πολλαπλότητα από το μηδέν στο D (NS). Γράφημα F (NS) τείνει στο μηδέν σε αυτό το σημείο, αλλά δεν ορίζεται εκεί. Υποδείξτε αυτό σχεδιάζοντας έναν κύκλο γύρω από το σημείο.
  • Μηδέν σε Β (NS) και μηδέν στο D (NS) έχουν την ίδια πολλαπλότητα. Το γράφημα προσεγγίζει κάποιο μη μηδενικό σημείο σε αυτήν την τιμή NSαλλά δεν ορίζεται σε αυτό. Υποδείξτε αυτό σχεδιάζοντας έναν κύκλο γύρω από το σημείο.
  • Μηδέν σε Β (NS) έχει χαμηλότερη πολλαπλότητα από το μηδέν στο D (NS). Υπάρχει ένα κάθετο ασύμπτωτο εδώ.