Περιεχόμενο

• Βήματα
• Μέθοδος 1 από 3: Πώς να λύσετε μια κυβική εξίσωση χωρίς σταθερό όρο
• Μέθοδος 2 από 3: Πώς να βρείτε ολόκληρες ρίζες χρησιμοποιώντας πολλαπλασιαστές
• Μέθοδος 3 από 3: Πώς να λύσετε μια εξίσωση χρησιμοποιώντας το διακριτικό

Σε μια κυβική εξίσωση, ο υψηλότερος εκθέτης είναι 3, μια τέτοια εξίσωση έχει 3 ρίζες (λύσεις) και έχει τη μορφή ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Ορισμένες κυβικές εξισώσεις δεν είναι τόσο εύκολο να επιλυθούν, αλλά αν εφαρμόσετε τη σωστή μέθοδο (με καλό θεωρητικό υπόβαθρο), μπορείτε να βρείτε τις ρίζες ακόμη και της πιο περίπλοκης κυβικής εξίσωσης - για αυτό χρησιμοποιήστε τον τύπο για την επίλυση της τετραγωνικής εξίσωσης, βρείτε ολόκληρες ρίζες, ή υπολογίστε το διακριτικό.

Βήματα

Μέθοδος 1 από 3: Πώς να λύσετε μια κυβική εξίσωση χωρίς σταθερό όρο

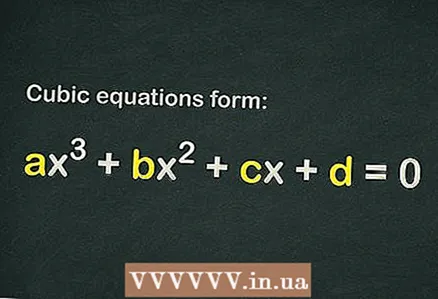1. 1 Μάθετε αν υπάρχει ελεύθερος όρος στην κυβική εξίσωση ρε{ displaystyle d}. Η κυβική εξίσωση έχει τη μορφή ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Για να θεωρηθεί μια εξίσωση κυβική, αρκεί μόνο ο όρος ${ displaystyle x ^ {3}}$ (δηλαδή, μπορεί να μην υπάρχουν καθόλου άλλα μέλη).
   • Εάν η εξίσωση έχει ελεύθερο όρο ${ displaystyle d}$, χρησιμοποιήστε διαφορετική μέθοδο.
   • Αν στην εξίσωση ${ displaystyle a = 0}$, δεν είναι κυβικό.
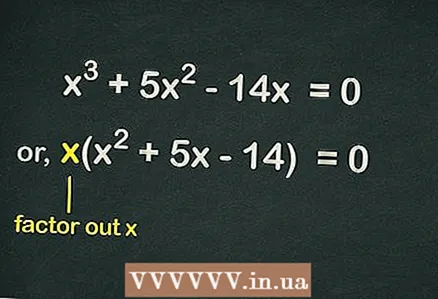2. 2 Βγάλτε από τις αγκύλες Χ{ displaystyle x}. Δεδομένου ότι δεν υπάρχει ελεύθερος όρος στην εξίσωση, κάθε όρος στην εξίσωση περιλαμβάνει τη μεταβλητή ${ displaystyle x}$... Αυτό σημαίνει αυτό ${ displaystyle x}$ μπορεί να αποκλειστεί από παρενθέσεις για να απλοποιηθεί η εξίσωση. Έτσι, η εξίσωση θα γραφτεί ως εξής: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Για παράδειγμα, δίνεται μια κυβική εξίσωση ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Βγάζω ${ displaystyle x}$ αγκύλες και πάρτε ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
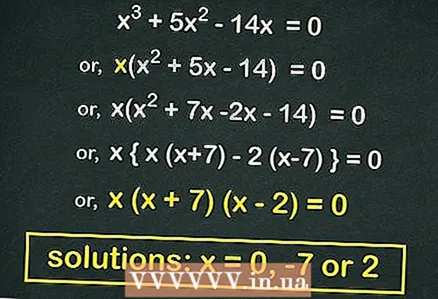3. 3 Συντελεστής (το προϊόν δύο διωνύμων) την τετραγωνική εξίσωση (αν είναι δυνατόν). Πολλές τετραγωνικές εξισώσεις της μορφής ${ displaystyle ax ^ {2} + bx + c = 0}$ μπορεί να παραγοντοποιηθεί. Μια τέτοια εξίσωση θα αποδειχθεί αν το βγάλουμε ${ displaystyle x}$ έξω από τις αγκύλες. Στο παράδειγμά μας:
   • Βγάλτε από τις αγκύλες ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Παράγοντας την τετραγωνική εξίσωση: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Εξισώστε κάθε κάδο σε ${ displaystyle 0}$... Οι ρίζες αυτής της εξίσωσης είναι ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Λύστε μια τετραγωνική εξίσωση χρησιμοποιώντας έναν ειδικό τύπο. Κάντε το αν η τετραγωνική εξίσωση δεν μπορεί να παραγοντοποιηθεί. Για να βρείτε δύο ρίζες μιας εξίσωσης, τις τιμές των συντελεστών ${ displaystyle a}$, ${ displaystyle β}$, ${ displaystyle c}$ υποκατάστατο στον τύπο ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Στο παράδειγμά μας, αντικαταστήστε τις τιμές των συντελεστών ${ displaystyle a}$, ${ displaystyle β}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) στον τύπο:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Πρώτη ρίζα:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Δεύτερη ρίζα:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Χρησιμοποιήστε μηδενικές και τετραγωνικές ρίζες ως λύσεις στην κυβική εξίσωση. Οι τετραγωνικές εξισώσεις έχουν δύο ρίζες, ενώ οι κυβικές τρεις. Έχετε ήδη βρει δύο λύσεις - αυτές είναι οι ρίζες της τετραγωνικής εξίσωσης. Εάν βάλετε το "x" έξω από τις αγκύλες, η τρίτη λύση θα ήταν ${ displaystyle 0}$.
   • Αν βγάλεις το "x" από τις αγκύλες, παίρνεις ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, δηλαδή, δύο παράγοντες: ${ displaystyle x}$ και μια τετραγωνική εξίσωση σε αγκύλες. Εάν κάποιος από αυτούς τους παράγοντες είναι ${ displaystyle 0}$, ολόκληρη η εξίσωση είναι επίσης ίση με ${ displaystyle 0}$.
   • Έτσι, δύο ρίζες μιας τετραγωνικής εξίσωσης είναι λύσεις μιας κυβικής εξίσωσης. Η τρίτη λύση είναι ${ displaystyle x = 0}$.

Μέθοδος 2 από 3: Πώς να βρείτε ολόκληρες ρίζες χρησιμοποιώντας πολλαπλασιαστές

1. 1 Βεβαιωθείτε ότι υπάρχει ένας ελεύθερος όρος στην κυβική εξίσωση ρε{ displaystyle d}. Αν σε εξίσωση της μορφής ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ υπάρχει δωρεάν μέλος ${ displaystyle d}$ (το οποίο δεν είναι ίσο με το μηδέν), δεν θα λειτουργήσει εάν τοποθετήσετε το "x" έξω από τις αγκύλες. Σε αυτήν την περίπτωση, χρησιμοποιήστε τη μέθοδο που περιγράφεται σε αυτήν την ενότητα.
   • Για παράδειγμα, δίνεται μια κυβική εξίσωση ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Για να πάρετε μηδέν στη δεξιά πλευρά της εξίσωσης, προσθέστε ${ displaystyle 6}$ και στις δύο πλευρές της εξίσωσης.
   • Η εξίσωση θα αποδειχθεί ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Οπως και ${ displaystyle d = 6}$, η μέθοδος που περιγράφεται στην πρώτη ενότητα δεν μπορεί να χρησιμοποιηθεί.
2. 2 Γράψτε τους συντελεστές του συντελεστή ένα{ displaystyle a} και δωρεάν μέλος ρε{ displaystyle d}. Δηλαδή, βρείτε τους παράγοντες του αριθμού στο ${ displaystyle x ^ {3}}$ και αριθμούς πριν από το πρόσημο ίσου. Θυμηθείτε ότι οι παράγοντες ενός αριθμού είναι οι αριθμοί που, όταν πολλαπλασιαστούν, παράγουν αυτόν τον αριθμό.
   • Για παράδειγμα, για να λάβετε τον αριθμό 6, πρέπει να πολλαπλασιαστείς ${ displaystyle 6 φορές 1}$ και ${ displaystyle 2 φορές 3}$... Τα νούμερα λοιπόν 1, 2, 3, 6 είναι παράγοντες του αριθμού 6.
   • Στην εξίσωση μας ${ displaystyle a = 2}$ και ${ displaystyle d = 6}$... Πολλαπλασιαστές 2 είναι 1 και 2... Πολλαπλασιαστές 6 είναι οι αριθμοί 1, 2, 3 και 6.
3. 3 Χωρίστε κάθε παράγοντα ένα{ displaystyle a} για κάθε παράγοντα ρε{ displaystyle d}. Ως αποτέλεσμα, παίρνετε πολλά κλάσματα και πολλούς ακέραιους αριθμούς. οι ρίζες της κυβικής εξίσωσης θα είναι ένας από τους ακέραιους αριθμούς ή η αρνητική τιμή ενός από τους ακέραιους αριθμούς.
   • Στο παράδειγμά μας, διαιρέστε τους παράγοντες ${ displaystyle a}$ (1 και 2) κατά παράγοντες ${ displaystyle d}$ (1, 2, 3 και 6). Θα πάρεις: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ και ${ displaystyle { frac {2} {3}}}$... Τώρα προσθέστε αρνητικές τιμές των κλασμάτων και των αριθμών που λαμβάνονται σε αυτήν τη λίστα: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ και ${ displaystyle - { frac {2} {3}}}$... Όλες οι ρίζες της κυβικής εξίσωσης είναι μερικοί αριθμοί από αυτήν τη λίστα.
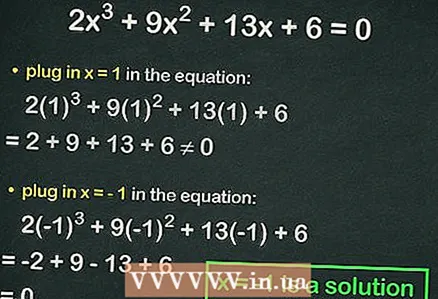4. 4 Συνδέστε ακέραιους αριθμούς στην κυβική εξίσωση. Εάν η ισότητα είναι αληθινή, ο υποκατεστημένος αριθμός είναι η ρίζα της εξίσωσης. Για παράδειγμα, αντικαταστήστε στην εξίσωση ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, δηλαδή δεν τηρείται η ισότητα. Σε αυτήν την περίπτωση, συνδέστε τον επόμενο αριθμό.
   • Υποκατάστατο ${ displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. Έτσι, ${ displaystyle -1}$ είναι ολόκληρη η ρίζα της εξίσωσης.
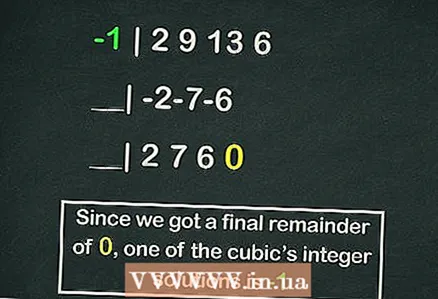5. 5 Χρησιμοποιήστε τη μέθοδο διαίρεσης πολυωνύμων με Το σχέδιο του Χόρνεργια να βρούμε πιο γρήγορα τις ρίζες της εξίσωσης. Κάντε το αν δεν θέλετε να αντικαταστήσετε με μη αυτόματο τρόπο τους αριθμούς στην εξίσωση. Στο σχήμα του Horner, οι ακέραιοι διαιρούνται με τις τιμές των συντελεστών της εξίσωσης ${ displaystyle a}$, ${ displaystyle β}$, ${ displaystyle c}$ και ${ displaystyle d}$... Εάν οι αριθμοί διαιρούνται ομοιόμορφα (δηλαδή, τα υπόλοιπα είναι ${ displaystyle 0}$), ένας ακέραιος αριθμός είναι η ρίζα της εξίσωσης.
   • Το σχήμα του Horner αξίζει ένα ξεχωριστό άρθρο, αλλά το παρακάτω είναι ένα παράδειγμα υπολογισμού μιας από τις ρίζες της κυβικής μας εξίσωσης χρησιμοποιώντας αυτό το σχήμα:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Το υπόλοιπο λοιπόν είναι ${ displaystyle 0}$, αλλά ${ displaystyle -1}$ είναι μία από τις ρίζες της εξίσωσης.

Μέθοδος 3 από 3: Πώς να λύσετε μια εξίσωση χρησιμοποιώντας το διακριτικό

1. 1 Γράψτε τις τιμές των συντελεστών της εξίσωσης ένα{ displaystyle a}, σι{ displaystyle β}, ντο{ displaystyle c} και ρε{ displaystyle d}. Σας συνιστούμε να γράψετε εκ των προτέρων τις τιμές των αναφερόμενων συντελεστών, ώστε να μην μπερδευτείτε στο μέλλον.
   • Για παράδειγμα, με την εξίσωση ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Σημειωσε ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ και ${ displaystyle d = -1}$... Θυμηθείτε ότι αν πριν ${ displaystyle x}$ δεν υπάρχει αριθμός, ο αντίστοιχος συντελεστής εξακολουθεί να υπάρχει και είναι ίσος με ${ displaystyle 1}$.
2. 2 Υπολογίστε το μηδενικό διαχωριστικό χρησιμοποιώντας έναν ειδικό τύπο. Για να λύσετε μια κυβική εξίσωση χρησιμοποιώντας το διακριτικό, πρέπει να εκτελέσετε έναν αριθμό δύσκολων υπολογισμών, αλλά αν εκτελέσετε σωστά όλα τα βήματα, αυτή η μέθοδος θα γίνει απαραίτητη για την επίλυση των πιο πολύπλοκων κυβικών εξισώσεων. Πρώτος υπολογισμός ${ displaystyle Delta _ {0}}$ (μηδενική διάκριση) είναι η πρώτη τιμή που χρειαζόμαστε. για να το κάνετε αυτό, αντικαταστήστε τις αντίστοιχες τιμές στον τύπο ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Ο διακριτικός είναι ένας αριθμός που χαρακτηρίζει τις ρίζες ενός πολυωνύμου (για παράδειγμα, η διάκριση μιας τετραγωνικής εξίσωσης υπολογίζεται από τον τύπο ${ displaystyle b ^ {2} -4ac}$).
   • Στην εξίσωση μας:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Υπολογίστε τον πρώτο διακριτικό χρησιμοποιώντας τον τύπο Δ1=2σι3−9ένασιντο+27ένα2ρε{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Πρώτο διακριτικό ${ displaystyle Delta _ {1}}$ - αυτή είναι η δεύτερη σημαντική τιμή. για να τον υπολογίσετε, συνδέστε τις αντίστοιχες τιμές στον καθορισμένο τύπο.
   • Στην εξίσωση μας:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Υπολογίζω:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Δηλαδή, βρείτε το διακριτικό της κυβικής εξίσωσης μέσω των ληφθέντων τιμών ${ displaystyle Delta _ {0}}$ και ${ displaystyle Delta _ {1}}$... Εάν η διάκριση μιας κυβικής εξίσωσης είναι θετική, η εξίσωση έχει τρεις ρίζες. Εάν η διάκριση είναι μηδέν, η εξίσωση έχει μία ή δύο ρίζες. εάν η διάκριση είναι αρνητική, η εξίσωση έχει μία ρίζα.
   • Μια κυβική εξίσωση έχει πάντα τουλάχιστον μία ρίζα, αφού η γραφική παράσταση αυτής της εξίσωσης τέμνει τον άξονα Χ τουλάχιστον σε ένα σημείο.
   • Στην εξίσωση μας ${ displaystyle Delta _ {0}}$ και ${ displaystyle Delta _ {1}}$ είναι ίσα ${ displaystyle 0}$, ώστε να μπορείτε εύκολα να υπολογίσετε ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Έτσι, η εξίσωση μας έχει μία ή δύο ρίζες.

5. 5 Υπολογίζω:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } δεξιά) div 2}}}$. ${ displaystyle C}$ - αυτή είναι η τελευταία σημαντική ποσότητα που βρέθηκε. θα σας βοηθήσει να υπολογίσετε τις ρίζες της εξίσωσης. Αντικαταστήστε τις τιμές στον καθορισμένο τύπο ${ displaystyle Delta _ {1}}$ και ${ displaystyle Delta _ {0}}$.
   • Στην εξίσωση μας:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Βρείτε τρεις ρίζες της εξίσωσης. Κάντε το με τον τύπο ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, όπου ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, αλλά ν είναι ίσο με 1, 2 ή 3... Αντικαταστήστε τις κατάλληλες τιμές σε αυτόν τον τύπο - ως αποτέλεσμα, θα έχετε τρεις ρίζες της εξίσωσης.
   • Υπολογίστε την τιμή χρησιμοποιώντας τον τύπο στο ν = 1, 2 ή 3και μετά ελέγξτε την απάντηση. Εάν λάβετε 0 όταν ελέγχετε την απάντησή σας, αυτή η τιμή είναι η ρίζα της εξίσωσης.
   • Στο παράδειγμά μας, υποκατάστατο 1 σε ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ και παρε 0, δηλ 1 είναι μία από τις ρίζες της εξίσωσης.