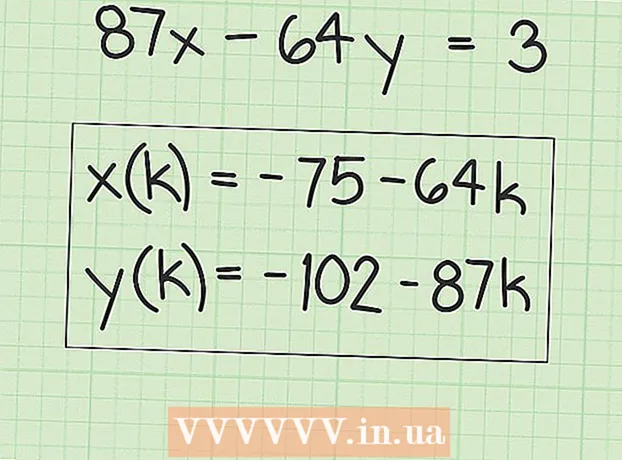
Περιεχόμενο

• Βήματα
• Μέρος 1 από 4: Πώς να γράψετε μια εξίσωση
• Μέρος 2 από 4: Πώς να γράψετε τον αλγόριθμο του Ευκλείδη
• Μέρος 3 από 4: Πώς να βρείτε μια λύση χρησιμοποιώντας τον αλγόριθμο του Ευκλείδη
• Μέρος 4 από 4: Βρείτε Άπειρες Άλλες Λύσεις

Για να λύσετε μια γραμμική εξίσωση Διοφαντίνης, πρέπει να βρείτε τις τιμές των μεταβλητών "x" και "y", που είναι ακέραιοι. Μια ακέραιη λύση είναι πιο πολύπλοκη από το συνηθισμένο και απαιτεί ένα συγκεκριμένο σύνολο ενεργειών. Αρχικά, πρέπει να υπολογίσετε τον μεγαλύτερο κοινό διαιρέτη (GCD) των συντελεστών και στη συνέχεια να βρείτε μια λύση. Αφού βρείτε μια ακέραιη λύση σε μια γραμμική εξίσωση, μπορείτε να χρησιμοποιήσετε ένα απλό μοτίβο για να βρείτε έναν άπειρο αριθμό άλλων λύσεων.

Βήματα

Μέρος 1 από 4: Πώς να γράψετε μια εξίσωση

1. 1 Γράψτε την εξίσωση σε τυπική μορφή. Μια γραμμική εξίσωση είναι μια εξίσωση στην οποία οι εκθέτες των μεταβλητών δεν υπερβαίνουν το 1. Για να λύσετε μια τέτοια γραμμική εξίσωση, γράψτε την πρώτα σε τυπική μορφή. Η τυπική μορφή γραμμικής εξίσωσης μοιάζει με αυτό: ${ displaystyle Ax + By = C}$, όπου ${ displaystyle A, B}$ και ${ displaystyle C}$ - ολόκληροι αριθμοί.
   • Εάν η εξίσωση δίνεται σε διαφορετική μορφή, φέρτε την σε τυπική μορφή χρησιμοποιώντας βασικές αλγεβρικές πράξεις. Για παράδειγμα, με την εξίσωση ${ displaystyle 23x + 4y -7x = -3y + 15}$... Δώστε παρόμοιους όρους και γράψτε την εξίσωση ως εξής: ${ displaystyle 16x + 7y = 15}$.
2. 2 Απλοποιήστε την εξίσωση (αν είναι δυνατόν). Όταν γράφετε την εξίσωση σε τυπική μορφή, κοιτάξτε τους συντελεστές ${ displaystyle A, B}$ και ${ displaystyle C}$... Εάν αυτές οι πιθανότητες έχουν GCD, διαιρέστε και τις τρεις πιθανότητες με αυτό. Η λύση σε μια τόσο απλουστευμένη εξίσωση θα είναι επίσης η λύση στην αρχική εξίσωση.
   • Για παράδειγμα, αν και οι τρεις συντελεστές είναι άρτιοι, διαιρέστε τους με τουλάχιστον 2. Για παράδειγμα:
     • ${ displaystyle 42x + 36y = 48}$ (όλα τα μέλη διαιρούνται με 2)
     • ${ displaystyle 21x + 18y = 24}$ (τώρα όλα τα μέλη διαιρούνται με το 3)
     • ${ displaystyle 7x + 6y = 8}$ (αυτή η εξίσωση δεν μπορεί πλέον να απλοποιηθεί)
3. 3 Ελέγξτε αν η εξίσωση μπορεί να λυθεί. Σε ορισμένες περιπτώσεις, μπορείτε αμέσως να δηλώσετε ότι η εξίσωση δεν έχει λύσεις. Εάν ο συντελεστής "C" δεν διαιρείται με το GCD των συντελεστών "A" και "B", η εξίσωση δεν έχει λύσεις.
   • Για παράδειγμα, εάν και οι δύο συντελεστές ${ displaystyle A}$ και ${ displaystyle B}$ είναι άρτιοι, τότε ο συντελεστής ${ displaystyle C}$ πρέπει να είναι ομοιόμορφο. Αλλα αν ${ displaystyle C}$ περίεργο, τότε δεν υπάρχει λύση.
     • Η εξίσωση ${ displaystyle 2x + 4y = 21}$ χωρίς ακέραιες λύσεις.
     • Η εξίσωση ${ displaystyle 5x + 10y = 17}$ δεν υπάρχουν ακέραιες λύσεις αφού η αριστερή πλευρά της εξίσωσης διαιρείται με το 5 και η δεξιά δεν είναι.

Μέρος 2 από 4: Πώς να γράψετε τον αλγόριθμο του Ευκλείδη

1. 1 Κατανοήστε τον αλγόριθμο του Ευκλείδη. Είναι μια σειρά επαναλαμβανόμενων διαιρέσεων στις οποίες το προηγούμενο υπόλοιπο χρησιμοποιείται ως επόμενος διαιρέτης. Ο τελευταίος διαιρέτης που διαιρεί τους αριθμούς ολοκληρωτικά είναι ο μεγαλύτερος κοινός διαιρέτης (GCD) των δύο αριθμών.
   • Για παράδειγμα, ας βρούμε το GCD των αριθμών 272 και 36 χρησιμοποιώντας τον αλγόριθμο του Ευκλείδη:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Διαιρέστε τον μεγαλύτερο αριθμό (272) με τον μικρότερο (36) και δώστε προσοχή στο υπόλοιπο (20).
     • ${ displaystyle 36 = 1 * 20 + 16}$ - διαιρέστε τον προηγούμενο διαιρέτη (36) με το προηγούμενο υπόλοιπο (20). Σημειώστε το νέο υπόλειμμα (16).
     • ${ displaystyle 20 = 1 * 16 + 4}$ - διαιρέστε τον προηγούμενο διαιρέτη (20) με το προηγούμενο υπόλοιπο (16). Σημειώστε το νέο υπόλειμμα (4).
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Διαιρέστε τον προηγούμενο διαιρέτη (16) με το προηγούμενο υπόλοιπο (4). Δεδομένου ότι το υπόλοιπο είναι 0, μπορούμε να πούμε ότι το 4 είναι το GCD των δύο αρχικών αριθμών 272 και 36.
2. 2 Εφαρμόστε τον αλγόριθμο του Ευκλείδη στους συντελεστές "Α" και "Β". Όταν γράφετε τη γραμμική εξίσωση σε τυπική μορφή, καθορίστε τους συντελεστές "Α" και "Β" και στη συνέχεια εφαρμόστε τον αλγόριθμο του Ευκλείδη για να βρείτε το GCD. Για παράδειγμα, δίνεται μια γραμμική εξίσωση ${ displaystyle 87x-64y = 3}$.
   • Ακολουθεί ο αλγόριθμος του Ευκλείδη για τους συντελεστές Α = 87 και Β = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Βρείτε τον μεγαλύτερο κοινό παράγοντα (GCD). Δεδομένου ότι ο τελευταίος διαιρέτης ήταν 1, το GCD 87 και το 64 είναι 1. Έτσι, τα 87 και 64 είναι πρώτοι αριθμοί σε σχέση μεταξύ τους.
4. 4 Αναλύστε το αποτέλεσμα. Όταν βρείτε τους συντελεστές gcd ${ displaystyle A}$ και ${ displaystyle B}$, συγκρίνετε το με τον συντελεστή ${ displaystyle C}$ την αρχική εξίσωση. Αν ${ displaystyle C}$ διαιρούμενο με gcd ${ displaystyle A}$ και ${ displaystyle B}$, η εξίσωση έχει μια ακέραιη λύση. αλλιώς η εξίσωση δεν έχει λύσεις.
   • Για παράδειγμα, η εξίσωση ${ displaystyle 87x-64y = 3}$ μπορεί να λυθεί επειδή το 3 διαιρείται με το 1 (gcd = 1).
   • Για παράδειγμα, ας υποθέσουμε ότι το GCD = 5. Το 3 δεν διαιρείται ομοιόμορφα με το 5, οπότε αυτή η εξίσωση δεν έχει ακέραιες λύσεις.
   • Όπως φαίνεται παρακάτω, αν μια εξίσωση έχει μία ακέραιη λύση, έχει επίσης άπειρο αριθμό άλλων ακέραιων λύσεων.

Μέρος 3 από 4: Πώς να βρείτε μια λύση χρησιμοποιώντας τον αλγόριθμο του Ευκλείδη

1. 1 Αριθμήστε τα βήματα για τον υπολογισμό του GCD. Για να βρείτε τη λύση σε μια γραμμική εξίσωση, πρέπει να χρησιμοποιήσετε τον Ευκλείδειο αλγόριθμο ως βάση για τη διαδικασία υποκατάστασης και απλοποίησης.
   • Ξεκινήστε με την αρίθμηση των βημάτων για τον υπολογισμό του GCD. Η διαδικασία υπολογισμού μοιάζει με αυτό:
     • ${ displaystyle { text {Βήμα 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Βήμα 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { κείμενο {Βήμα 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { κείμενο {Βήμα 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { κείμενο {Βήμα 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { κείμενο {Βήμα 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { κείμενο {Βήμα 7}}: 2 = (2 * 1) +0}$
2. 2 Δώστε προσοχή στο τελευταίο βήμα, όπου υπάρχει το υπόλοιπο. Ξαναγράψτε την εξίσωση για αυτό το βήμα για να απομονώσετε το υπόλοιπο.
   • Στο παράδειγμά μας, το τελευταίο βήμα με το υπόλοιπο είναι το βήμα 6. Το υπόλοιπο είναι 1. Ξαναγράψτε την εξίσωση στο βήμα 6 ως εξής:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Απομονώστε το υπόλοιπο του προηγούμενου βήματος. Αυτή η διαδικασία είναι ένα βήμα-βήμα "ανέβασμα". Κάθε φορά που θα απομονώνετε το υπόλοιπο στην εξίσωση στο προηγούμενο βήμα.
   • Απομονώστε το υπόλοιπο της εξίσωσης στο Βήμα 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ ή ${ displaystyle 2 = 5-3}$
4. 4 Αντικαταστήστε και απλοποιήστε. Παρατηρήστε ότι η εξίσωση στο βήμα 6 περιέχει τον αριθμό 2 και στην εξίσωση στο βήμα 5, ο αριθμός 2 είναι απομονωμένος. Αντί για "2" στην εξίσωση στο βήμα 6, αντικαταστήστε την έκφραση στο βήμα 5:
   • ${ displaystyle 1 = 3-2}$ (εξίσωση του βήματος 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (αντί για 2, μια έκφραση αντικαταστάθηκε)
   • ${ displaystyle 1 = 3-5 + 3}$ (ανοιχτές αγκύλες)
   • ${ displaystyle 1 = 2 (3) -5}$ (απλοποιημένο)
5. 5 Επαναλάβετε τη διαδικασία αντικατάστασης και απλοποίησης. Επαναλάβετε την περιγραφόμενη διαδικασία, μετακινώντας τον Ευκλείδειο αλγόριθμο με αντίστροφη σειρά. Κάθε φορά που θα ξαναγράψετε την εξίσωση από το προηγούμενο βήμα και θα την συνδέσετε στην τελευταία εξίσωση που θα λάβετε.
   • Το τελευταίο βήμα που εξετάσαμε ήταν το βήμα 5. Πηγαίνετε στο βήμα 4 και απομονώστε το υπόλοιπο στην εξίσωση για αυτό το βήμα:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Αντικαταστήστε αυτήν την έκφραση με το "3" στην τελευταία εξίσωση:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Συνεχίστε με τη διαδικασία υποκατάστασης και απλοποίησης. Αυτή η διαδικασία θα επαναληφθεί μέχρι να φτάσετε στο αρχικό βήμα του Ευκλείδειου αλγορίθμου. Ο στόχος της διαδικασίας είναι να γραφτεί η εξίσωση με τους συντελεστές 87 και 64 της αρχικής εξίσωσης που πρέπει να λυθεί. Στο παράδειγμά μας:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (αντικατέστησε την έκφραση από το βήμα 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (αντικατέστησε την έκφραση από το βήμα 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (αντικατέστησε την έκφραση από το βήμα 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Ξαναγράψτε την εξίσωση που προκύπτει σύμφωνα με τους αρχικούς συντελεστές. Όταν επιστρέψετε στο πρώτο βήμα του Ευκλείδειου αλγορίθμου, θα δείτε ότι η εξίσωση που προκύπτει περιέχει δύο συντελεστές της αρχικής εξίσωσης. Ξαναγράψτε την εξίσωση έτσι ώστε η σειρά των όρων της να ταιριάζει με τους συντελεστές της αρχικής εξίσωσης.
   • Στο παράδειγμά μας, η αρχική εξίσωση ${ displaystyle 87x-64y = 3}$... Επομένως, ξαναγράψτε την εξίσωση που προκύπτει έτσι ώστε οι συντελεστές να ευθυγραμμιστούν.Δώστε ιδιαίτερη προσοχή στον συντελεστή "64". Στην αρχική εξίσωση, αυτός ο συντελεστής είναι αρνητικός και στον Ευκλείδειο αλγόριθμο, είναι θετικός. Επομένως, ο παράγοντας 34 πρέπει να γίνει αρνητικός. Η τελική εξίσωση θα γραφτεί ως εξής:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Εφαρμόστε τον κατάλληλο πολλαπλασιαστή για να βρείτε μια λύση. Σημειώστε ότι στο παράδειγμά μας, GCD = 1, άρα η τελική εξίσωση είναι 1. Αλλά η αρχική εξίσωση (87x-64y) είναι 3. Επομένως, όλοι οι όροι στην τελική εξίσωση πρέπει να πολλαπλασιαστούν με 3 για να πάρουμε τη λύση:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Γράψτε την ακέραιη λύση στην εξίσωση. Οι αριθμοί που πολλαπλασιάζονται με τους συντελεστές της αρχικής εξίσωσης είναι οι λύσεις σε αυτήν την εξίσωση.
   • Στο παράδειγμά μας, γράψτε τη λύση ως ζεύγος συντεταγμένων: ${ displaystyle (x, y) = ( - 75, -102)}$.

Μέρος 4 από 4: Βρείτε Άπειρες Άλλες Λύσεις

1. 1 Κατανοήστε ότι υπάρχει άπειρος αριθμός λύσεων. Εάν μια γραμμική εξίσωση έχει μία ακέραιη λύση, τότε πρέπει να έχει άπειρα πολλές ακέραιες λύσεις. Ακολουθεί μια γρήγορη απόδειξη (σε αλγεβρική μορφή):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (αν προσθέσετε "B" στο "x" και αφαιρέσετε "A" από "y", η τιμή της αρχικής εξίσωσης δεν θα αλλάξει)
2. 2 Καταγράψτε τις αρχικές τιμές x και y. Το πρότυπο για τον υπολογισμό των επόμενων (άπειρων) λύσεων ξεκινά με τη μόνη λύση που έχετε ήδη βρει.
   • Στο παράδειγμά μας, η λύση είναι ένα ζεύγος συντεταγμένων ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Προσθέστε τον παράγοντα "B" στην τιμή "x". Κάντε αυτό για να βρείτε τη νέα τιμή x.
   • Στο παράδειγμά μας, x = -75 και B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Έτσι, η νέα τιμή "x": x = -139.
4. 4 Αφαιρέστε τον παράγοντα "A" από την τιμή "y". Για να μην αλλάξει η τιμή της αρχικής εξίσωσης, όταν προσθέτετε έναν αριθμό στο "x", πρέπει να αφαιρέσετε έναν άλλο αριθμό από το "y".
   • Στο παράδειγμά μας, y = -102 και A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Έτσι, η νέα τιμή για "y": y = -189.
   • Το νέο ζεύγος συντεταγμένων θα γραφτεί ως εξής: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Ελέγξτε τη λύση. Για να επαληθεύσετε ότι το νέο ζεύγος συντεταγμένων είναι λύση στην αρχική εξίσωση, συνδέστε τις τιμές στην εξίσωση.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Δεδομένου ότι τηρείται η ισότητα, η απόφαση είναι σωστή.
6. 6 Γράψτε εκφράσεις για να βρείτε πολλές λύσεις. Οι τιμές "x" θα είναι ίσες με την αρχική λύση συν τυχόν πολλαπλάσιο του παράγοντα "B". Αυτό μπορεί να γραφτεί ως η ακόλουθη έκφραση:
   • x (k) = x + k (B), όπου "x (k)" είναι το σύνολο των τιμών "x" και "x" είναι η αρχική (πρώτη) τιμή του "x" που βρήκατε.
     • Στο παράδειγμά μας:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), όπου y (k) είναι το σύνολο των τιμών y και y είναι η αρχική (πρώτη) τιμή y που βρήκατε.
     • Στο παράδειγμά μας:
     • ${ displaystyle y (k) = - 102-87k}$