Περιεχόμενο

• Για να πας

Μια τριγωνομετρική εξίσωση είναι μια εξίσωση με μία ή περισσότερες τριγωνομετρικές συναρτήσεις της μεταβλητής τριγωνομετρικής καμπύλης x. Η επίλυση για x σημαίνει εύρεση των τιμών των τριγωνομετρικών καμπυλών των οποίων οι τριγωνομετρικές συναρτήσεις προκαλούν την αλήθεια της τριγωνομετρικής εξίσωσης.

• Οι απαντήσεις ή οι τιμές των καμπυλών λύσης εκφράζονται σε μοίρες ή ακτίνια. Παραδείγματα:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 μοίρες; x = 37,12 μοίρες; x = 178,37 μοίρες

• Σημείωση: Στον κύκλο μονάδας, οι τριγωνομετρικές συναρτήσεις οποιασδήποτε καμπύλης είναι ίσες με τις τριγωνομετρικές συναρτήσεις της αντίστοιχης γωνίας. Ο κύκλος μονάδας καθορίζει όλες τις τριγωνομετρικές συναρτήσεις της μεταβλητής καμπύλης x. Χρησιμοποιείται επίσης ως απόδειξη για την επίλυση βασικών τριγωνομετρικών εξισώσεων και ανισοτήτων.
• Παραδείγματα τριγωνομετρικών εξισώσεων:
  • sin x + sin 2x = 1/2; μαύρισμα x + κούνια x = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Ο κύκλος μονάδας.
   • Αυτός είναι ένας κύκλος με Radius = 1, όπου το O είναι η προέλευση. Ο κύκλος μονάδας ορίζει 4 κύριες τριγωνομετρικές συναρτήσεις της μεταβλητής καμπύλης x, οι οποίες την περιβάλλουν αριστερόστροφα.
   • Όταν η καμπύλη με τιμή x διαφέρει στον κύκλο μονάδας, τότε κρατά:
   • Ο οριζόντιος άξονας OAx ορίζει την τριγωνομετρική συνάρτηση f (x) = cos x.
   • Ο κατακόρυφος άξονας OBy ορίζει την τριγωνομετρική συνάρτηση f (x) = sin x.
   • Ο κατακόρυφος άξονας AT καθορίζει την τριγωνομετρική συνάρτηση f (x) = μαύρισμα x.
   • Ο οριζόντιος άξονας BU καθορίζει την τριγωνομετρική συνάρτηση f (x) = cot x.

• Ο κύκλος μονάδας χρησιμοποιείται επίσης για την επίλυση βασικών τριγωνομετρικών εξισώσεων και τυπικών τριγωνομετρικών ανισοτήτων, λαμβάνοντας υπόψη τις διάφορες θέσεις της καμπύλης x στον κύκλο.

Για να πας

1. Κατανοήστε τη μέθοδο λύσης.
   • Για να λύσετε μια τριγωνομετρική εξίσωση τη μετατρέπετε σε μία ή περισσότερες βασικές τριγωνομετρικές εξισώσεις. Η επίλυση τριγωνομετρικών εξισώσεων οδηγεί τελικά στην επίλυση 4 βασικών τριγωνομετρικών εξισώσεων.
2. Μάθετε πώς να επιλύετε βασικές τριγωνομετρικές εξισώσεις.
   • Υπάρχουν 4 βασικές τριγωνομετρικές εξισώσεις:
   • sin x = α; cos x = α
   • μαύρισμα x = α; κούνια x = α
   • Μπορείτε να επιλύσετε τις βασικές τριγωνομετρικές εξισώσεις μελετώντας τις διάφορες θέσεις της καμπύλης x στον τριγωνομετρικό κύκλο και χρησιμοποιώντας έναν τριγωνομετρικό πίνακα μετατροπής (ή αριθμομηχανή). Για να κατανοήσετε πλήρως πώς να επιλύσετε αυτές και παρόμοιες βασικές τριγωνομετρικές εξισώσεις, διαβάστε το ακόλουθο βιβλίο: "Τριγωνομετρία: Επίλυση τριγωνομετρικών εξισώσεων και ανισοτήτων" (Amazon E-book 2010).
   • Παράδειγμα 1. Επίλυση για sin x = 0,886. Ο πίνακας μετατροπής (ή η αριθμομηχανή) δίνει την απάντηση: x = Pi / 3. Ο τριγωνομετρικός κύκλος δίνει μια άλλη καμπύλη (2Pi / 3) με την ίδια τιμή για το ημίτονο (0,886). Ο τριγωνομετρικός κύκλος παρέχει επίσης ένα άπειρο απαντήσεων που ονομάζονται εκτεταμένες απαντήσεις.
   • x1 = Pi / 3 + 2k.Pi και x2 = 2Pi / 3. (Απαντήσεις εντός περιόδου (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi και x2 = 2Pi / 3 + 2k Pi. (Λεπτομερείς απαντήσεις).
   • Παράδειγμα 2. Επίλυση: cos x = -1/2. Οι αριθμομηχανές δίνουν x = 2 Pi / 3. Ο τριγωνομετρικός κύκλος δίνει επίσης x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi και x2 = - 2Pi / 3. (Απαντήσεις για την περίοδο (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi και x2 = -2Pi / 3 + 2k.Pi. (Εκτεταμένες απαντήσεις)
   • Παράδειγμα 3. Επίλυση: μαύρισμα (x - Pi / 4) = 0.
   • x = Pi / 4; (Απάντηση)
   • x = Pi / 4 + k Pi; (Εκτεταμένη απάντηση)
   • Παράδειγμα 4. Λύστε: κούνια 2x = 1,732. Οι αριθμομηχανές και ο τριγωνομετρικός κύκλος δίνουν:
   • x = Pi / 12; (Απάντηση)
   • x = Pi / 12 + k Pi; (Εκτεταμένες απαντήσεις)
3. Μάθετε τους μετασχηματισμούς που χρησιμοποιούνται για την επίλυση τριγωνομετρικών εξισώσεων.
   • Για να μετατρέψετε μια δεδομένη τριγωνομετρική εξίσωση σε τυπικές τριγωνομετρικές εξισώσεις, χρησιμοποιήστε τυπικές αλγεβρικές μετατροπές (παραγοντοποίηση, κοινός παράγοντας, πολυώνυμα ...), ορισμούς και ιδιότητες τριγωνομετρικών συναρτήσεων και τριγωνομετρικών ταυτοτήτων. Υπάρχουν περίπου 31, 14 από τα οποία είναι τριγωνομετρικές ταυτότητες, από 19 έως 31, που ονομάζονται επίσης ταυτότητες μετασχηματισμού, επειδή χρησιμοποιούνται στη μετατροπή τριγωνομετρικών εξισώσεων. Δείτε το παραπάνω βιβλίο.
   • Παράδειγμα 5: Η τριγωνομετρική εξίσωση: sin x + sin 2x + sin 3x = 0 μπορεί να μετατραπεί σε προϊόν βασικών τριγωνομετρικών εξισώσεων χρησιμοποιώντας τριγωνομετρικές ταυτότητες: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Οι βασικές τριγωνομετρικές εξισώσεις που πρέπει να επιλυθούν είναι: cos x = 0; sin (3x / 2) = 0; και cos (x / 2) = 0.
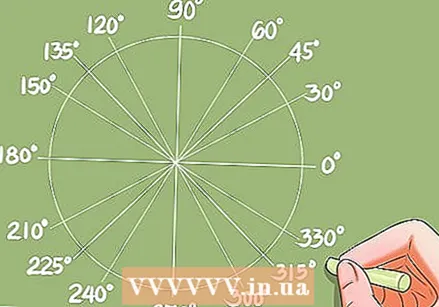4. Βρείτε τις καμπύλες για τις οποίες είναι γνωστές οι τριγωνομετρικές συναρτήσεις.
   • Για να μπορέσετε να μάθετε πώς να επιλύετε τριγωνομετρικές εξισώσεις, πρέπει να γνωρίζετε πώς να βρείτε γρήγορα τις καμπύλες για τις οποίες είναι γνωστές οι τριγωνομετρικές συναρτήσεις. Οι τιμές μετατροπής των καμπυλών (ή γωνιών) μπορούν να προσδιοριστούν με τριγωνομετρικούς πίνακες ή την αριθμομηχανή.
   • Παράδειγμα: Επίλυση για cos x = 0,732. Η αριθμομηχανή δίνει τη λύση x = 42,95 μοίρες. Ο κύκλος μονάδας δίνει άλλες καμπύλες με την ίδια τιμή για το συνημίτονο.
5. Σχεδιάστε το τόξο της απάντησης στον κύκλο μονάδας.
   • Μπορείτε να δημιουργήσετε ένα γράφημα για να απεικονίσετε τη λύση στον κύκλο της μονάδας. Τα τελικά σημεία αυτών των καμπυλών είναι κανονικά πολύγωνα στον τριγωνομετρικό κύκλο. Μερικά παραδείγματα:
   • Τα τελικά σημεία της καμπύλης x = Pi / 3 + k. Pi / 2 είναι ένα τετράγωνο στον κύκλο μονάδας.
   • Οι καμπύλες του x = Pi / 4 + k.Pi / 3 αντιπροσωπεύονται από τις συντεταγμένες ενός εξαγώνου στον κύκλο μονάδας.
6. Μάθετε πώς να επιλύετε τριγωνομετρικές εξισώσεις.
   • Εάν η δεδομένη τριγωνομετρική εξίσωση περιέχει μόνο μία τριγωνομετρική συνάρτηση, λύστε την ως τυπική τριγωνομετρική εξίσωση. Εάν η δεδομένη εξίσωση περιέχει δύο ή περισσότερες τριγωνομετρικές συναρτήσεις, υπάρχουν 2 μέθοδοι λύσης, ανάλογα με τις επιλογές μετατροπής της εξίσωσης.
     • A. Μέθοδος 1.
   • Μετατρέψτε την τριγωνομετρική εξίσωση σε ένα προϊόν της φόρμας: f (x) .g (x) = 0 ή f (x) .g (x) .h (x) = 0, όπου f (x), g (x) και h (x) είναι βασικές τριγωνομετρικές εξισώσεις.
   • Παράδειγμα 6. Επίλυση: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Λύση. Αντικαταστήστε το sin 2x στην εξίσωση χρησιμοποιώντας την ταυτότητα: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Στη συνέχεια, λύστε 2 τυπικές τριγωνομετρικές συναρτήσεις: cos x = 0 και (sin x + 1) = 0.
   • Παράδειγμα 7. Επίλυση: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • Λύση: Μετατρέψτε το σε προϊόν, χρησιμοποιώντας τις τριγωνομετρικές ταυτότητες: cos 2x (2cos x + 1) = 0. Τώρα λύστε τις 2 βασικές τριγωνομετρικές εξισώσεις: cos 2x = 0 και (2cos x + 1) = 0.
   • Παράδειγμα 8. Επίλυση: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Λύση: Μετατρέψτε το σε προϊόν, χρησιμοποιώντας τις τριγωνομετρικές ταυτότητες: -cos 2x * (2sin x + 1) = 0. Τώρα λύστε τις 2 βασικές τριγωνομετρικές εξισώσεις: cos 2x = 0 και (2sin x + 1) = 0.
     • Β. Προσέγγιση 2.
   • Μετατρέπει την εξίσωση trig σε εξίσωση trig με μία μόνο μοναδική συνάρτηση trig ως μεταβλητή. Υπάρχουν μερικές συμβουλές για το πώς να επιλέξετε μια κατάλληλη μεταβλητή. Κοινές μεταβλητές είναι: sin x = t; cos x = t; cos 2x = t, μαύρισμα x = t και μαύρισμα (x / 2) = t.
   • Παράδειγμα 9. Επίλυση: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Λύση. Στην εξίσωση, αντικαταστήστε (cos ^ 2x) με (1 - sin ^ 2x) και απλοποιήστε την εξίσωση:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Τώρα χρησιμοποιήστε sin x = t. Η εξίσωση γίνεται: 5t ^ 2 - 4t - 9 = 0. Πρόκειται για μια τετραγωνική εξίσωση με 2 ρίζες: t1 = -1 και t2 = 9/5. Μπορούμε να απορρίψουμε το δεύτερο t2, γιατί> 1. Τώρα λύστε για: t = sin = -1 -> x = 3Pi / 2.
   • Παράδειγμα 10. Λύστε: μαύρισμα x + 2 μαύρισμα ^ 2 x = κούνια x + 2.
   • Λύση. Χρησιμοποιήστε μαύρισμα x = t. Μετατρέψτε τη δεδομένη εξίσωση σε εξίσωση με t ως μεταβλητή: (2t + 1) (t ^ 2 - 1) = 0. Λύστε για t από αυτό το προϊόν και, στη συνέχεια, λύστε την τυπική τριγωνομετρική εξίσωση tan x = t για x.
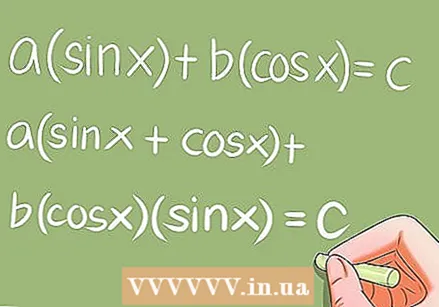7. Λύστε ειδικές τριγωνομετρικές εξισώσεις.
   • Υπάρχουν μερικές ειδικές τριγωνομετρικές εξισώσεις που απαιτούν συγκεκριμένες μετατροπές. Παραδείγματα:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
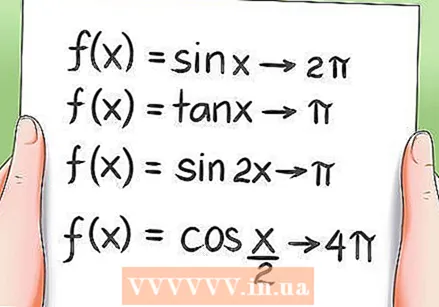8. Μάθετε τις περιοδικές ιδιότητες των τριγωνομετρικών συναρτήσεων.
   • Όλες οι τριγωνομετρικές συναρτήσεις είναι περιοδικές, πράγμα που σημαίνει ότι επιστρέφουν στην ίδια τιμή μετά από μια περιστροφή σε μια περίοδο. Παραδείγματα:
     • Η συνάρτηση f (x) = sin x έχει 2Pi ως τελεία.
     • Η συνάρτηση f (x) = tan x έχει Pi ως τελεία.
     • Η συνάρτηση f (x) = sin 2x έχει Pi ως τελεία.
     • Η συνάρτηση f (x) = cos (x / 2) έχει 4Pi ως τελεία.
   • Εάν η περίοδος καθορίζεται στις ασκήσεις / δοκιμές, τότε πρέπει απλώς να βρείτε τις καμπύλες x εντός αυτής της περιόδου.
   • ΣΗΜΕΙΩΣΗ: Η επίλυση τριγωνομετρικών εξισώσεων είναι δύσκολη και συχνά οδηγεί σε λάθη και λάθη. Επομένως, οι απαντήσεις πρέπει να ελέγχονται προσεκτικά. Μετά την επίλυση, μπορείτε να ελέγξετε τις απαντήσεις χρησιμοποιώντας μια αριθμομηχανή γραφημάτων, για άμεση αναπαράσταση της δεδομένης τριγωνομετρικής εξίσωσης R (x) = 0. Οι απαντήσεις (ως τετραγωνική ρίζα) δίνονται σε δεκαδικά ψηφία. Για παράδειγμα, το Pi έχει τιμή 3,14